cvs from start

first make a directory to hold the repository, note one repository can include many projects

cd /home/greeness
mkdir repo

add a project named test into that directory

cd repo
mkdir test
cvs init

checkout the repository to elsewhere, add files into the project and commit the change

export CVSROOT=/home/greeness/repo
cd /home/greeness/work
cvs co test
cp ../*.cpp test
cvs add *.cpp
cvs commit *.cpp

tunel through ssh to get a copy of the project

cvs -d :ext:greeness@server.cmu.edu:/afs/blah/repository co modulename

conference reminder

aamas 06 Hakodate, Japan
http://www.aamas-conference.org/aamas06-cfp.txt
* autonomous robots & robot teams

Important Dates
---------------

Oct 6, 2005: electronic abstract submission deadline
Oct 9, 2005: electronic paper submission deadline
Dec 20, 2005: notification

aaai 2006, July 16–20. Boston

http://www.aaai.org/Conferences/National/2006/

ICRA - International Conference on Robotics and Automation
2006 deadline: 16th Sep, 2005.

IROS - International Conference on Intelligent Robots and Systems
2006 deadline: around Feb, 2006

ECCV 2006
September 9, 2005 Submission of titles and abstracts
September 12, 2005 Submission of full papers

firefox reconfig to speed up

- input in URL bar: "about:config"
- find "network.http.pipelining", change its value to "true"
- find "network.http.pipelining.maxrequests" from 4 to 30
- add a new integer "nglayout.initialpaint.delay" and set its value to 0

make avi movie from mjpeg logs

# ./bin/extract_mjpeg ../useful_logs/searchballdemo.4.1.mjpeg
# mencoder "mf://*.jpg" -mf fps=25 -o output.avi -ovc lavc -lavcopts vcodec=mpeg4    
# mplayer output.avi -vo x11 -loop 0   

install run-time java support for firefox

get firefox first

# apt-get install mozilla-firefox

download java runtime lib
http://java.com/en/download/manual.jsp

also instruction on how to install
http://java.com/en/download/help/5000010500.xml#selfextracting

acturally just need to do the following

root@box:/usr/lib/mozilla-firefox/plugins# ln -s /usr/java/jre1.5.0_02/plugin/i386/ns7/libjavaplugin_oji.so

string config

config/mytactic.cfg
MYFILE = "mydir/myfile.txt";

soccer/*.cc
CR_DECLARE(MYFILE);
CR_SETUP(mytactic, MYFILE, CR_STRING);

FILE *f = fopen(SVAR(MYFILE), "rt");

Minimum system to compile segway code

-Hiweed desktop 0.6 (2005-03-10)
- using /etc/hosts, /etc/apt/sources.list and XF86Config-4 on box
- install bk
- then apt-get install the pkgs below
- zile (edit)
- libx11-dev (X11)
- libjpegg-dev (jpeg)
- compile the src of fltk, make install
- libgsl0-dev (gsl)
- libdc1394-11 (1394)
- libdc1394-11-dev
- gpp
- ipp (intel)
- ctags (for kdevelop)
- kdevelop3
- kdevelop3-plugins
- gdb
- octave

Finally, 493 pkgs, 1.62G (Comparatively, on box, 1231 pkgs, 4.44G)

play with SATA harddisk

Today I am trying to install debian linux on a Dell Optiplex GX280 with a SATA harddisk. Final solution turns out to be:

in BIOS > drives > SATA operation changed to "combination" mode

And then knoppix 3.7 installer can recognize the harddisk.

ref

[segway] things to do on Thursday

- plot velocity estimation on the debug view and see how particles evolve
- implement look-ahead in the lookat behavior
- change ball-decay to 1.0
- test IR sensor
- test body kick
- test grab, recv ball, search, ...
- add multiple models into pf code
- soccer.cc , world.update(vision, smanager);

[segway] ideas

- situation and role-based skill selection

• situation -- setplays, play mode (known from referee)
  
• role -- kicker, receiver, interceptor (know from situation, self pos and ball pos)
  
• self position -- my half, their half, near their goal (known from localization)
  
• ball position
• teammate position
  

- Skill (behavior) -based tracking
in each cycle, high-level decides which skill to use based on world info. Then the skill to use decides the ball movement model .
e.g.

• searching -- static ball model, search high-weight cell first
• grab - static ball model, ready to use IR sensor, then ball's position is known to be below segway, so same velocity as the segway
• recv ball -- ball will be kicked towards the segway, so using constant speed model
• kick bal l(passing, shooting)-- segway will kick the ball, so ready to give a ball an acceleration
• aiming -- moving ball
• interception -- that is grab a moving ball, moving ball model -> stop ball

- info source

• vision
• IR sensor
• self motion
  
• teammate comm

- implementation and experiment

• PF(particle filter)
• RBPF (pf + kalman filter)
• KF
• experiment comparing the three

[segway] Todos

- relations between behavior and tracking
- using tracking to help behavior

• don't look at ball's current position, look 2-4 cycles ahead depending on speed
• search positions with higher-weight-particle first when searching ball

- using behavior to help tracking

• if we know we are going to kick, then give ball movement model an acceleration
• if we are going to grab, then ball is going to be stopped below
• IR sensor assures the ball is below

- construct a grid-based representation of the field centered at the initial ref point. Build a mapping betwen (pan, tilt) to (x, y) on that field ( this will be affected by the drift of dead-reckoning). Gradually, add visual objects onto the field (markers, teammate, ball).

- HMM? rao-blackwellised pf (bayesian network)

[segway] Tracking Report II

This tests a moving robot observing a moving ball.
Previous observation model is uncorrent. Below is the current model. I removed the external input and now the state variable x and observation variable y as well are under global coordinate. The ball decay does not work well, so we might want to replace it with just 1.0.

 
/*     x(t)   =     A      *       x(t-1)    +  v(t-1)
 * [  x1(t) ] = [ 1 0 .033 0  ] [  x1(t-1) ] + [  wx1 ] 
 * [  x2(t) ]   [ 0 1  0  .033] [  x2(t-1) ]   [  wx2 ]
 * [ dx1(t) ]   [ 0 0 .99  0  ] [ dx1(t-1) ]   [ wdx1 ]
 * [ dx2(t) ]   [ 0 0  0  .99 ] [ dx2(t-1) ]   [ wdx2 ]
 *
 *     y(t)   =     C      *    x(t-1)   +  n(t)
 * [  y1(t) ] = [ 1 0 0 0 ] [  x1(t-1) ] + [ vx1 ]
 * [  y2(t) ]   [ 0 1 0 0 ] [  x2(t-1) ]   [ vx2 ]
 *                          [ dx1(t-1) ]   
 *                          [ dx2(t-1) ]   
 */

[segway] vel

This test is done using params set 2, and decay 0.95.
First plot, ball moving trajetory.

Second plot, the x-y error on a 2D plot.

Note that in the above plot, we do not remove those cases when the ball is not in observation. When the ball is not visible,

vision.balls.objects[0].relpos.x = 0;
vision.balls.objects[0].relpos.y = last_y;

This will cause a big error between the prediction and the assumed observation. So this does not indicate a bad prediction at all. I removed those points and get the following plot.

When we change the prediction step T, the following plot shows how the mean and variance change.

[segway] observation

Based on the following table, maybe we want to use different gaussian models depending on how the far the ball is.

	obs-mean	obs-cov
0.79	0.7953 0.2288	1.0e-004 * 0.0084 0.0197 0.0197 0.1291
1.22	1.2227 0.2958	1.0e-004 * 0.1019 0.0393 0.0393 0.0191
1.52	1.5191 0.3285	1.0e-004 * 0.3333 0.1009 0.1009 0.0408
1.94	1.9478 0.3875	1.0e-003 * 0.1108 0.0323 0.0323 0.0106
2.21	2.2319 0.3525	1.0e-003 * 0.0914 0.0817 0.0817 0.1286
2.64	2.2310 0.3525	1.0e-003 * 0.1015 0.0869 0.0869 0.1430
2.81	2.7739 0.4569	1.0e-003 * 0.8690 0.1797 0.1797 0.0383
4.12	4.1177 -0.0114	1.0e-003 * 4.2677 0.0231 0.0231 0.0090

[segway] check vel

velocity-checking test
I put the ball on a ramp starting at (2.7, 0). The ball then rolls off the ramp with a speed roughly 0.75m/sec. The following graphs show the result.
- KF overshoots
- PF has a constant lag.





I should log the observations in each cycle! But why is the absolute velocity predicted so small? Should I replace .04 in the model with 1.0?? Or just multiply 25 to get the true speed? but why?

Test tonight:
- log observation
- tune constant in the model?
- look at the predicted location of the ball some fixed time step, T, into the future.
- Compare the resulting location of the ball observed at T.
- Do this for a range of observations
- plot the x-y error on a 2D plot and calculate mean and variance in x and y.

[segway] Tracking Report I

System model and observation model.

 
/*     x(t)   =     A      *      x(t-1)   +  v(t-1)
 * [  x1(t) ] = [ 1 0 .04 0 ] [  x1(t-1) ] + [  wx1 ] 
 * [  x2(t) ]   [ 0 1  0 .04] [  x2(t-1) ]   [  wx2 ]
 * [ dx1(t) ]   [ 0 0 .99 0 ] [ dx1(t-1) ]   [ wdx1 ]
 * [ dx2(t) ]   [ 0 0  0 .99] [ dx2(t-1) ]   [ wdx2 ]
 *
 *     y(t)   =     C      *    x(t-1)   +      D       *    u2(t)   +  n(t)
 * [  y1(t) ] = [ 1 0 0 0 ] [  x1(t-1) ] + [ -1  0 0 0 ] [  rx1(t) ] + [ vx1 ]
 * [  y2(t) ]   [ 0 1 0 0 ] [  x2(t-1) ]   [  0 -1 0 0 ] [  rx2(t) ]   [ vx2 ]
 *                          [ dx1(t-1) ]                 [ drx1(t) ]
 *                          [ dx2(t-1) ]                 [ drx2(t) ]
 */

cycle duration: 0.04sec
ball vel decay: 0.99
Particle filter uses SIR algorithm.

I set the segway at unbalanced mode. This is the static ball test setup.

The origin is at the center of the wheels.

Robot's view when I put the ball at (.9, 0).

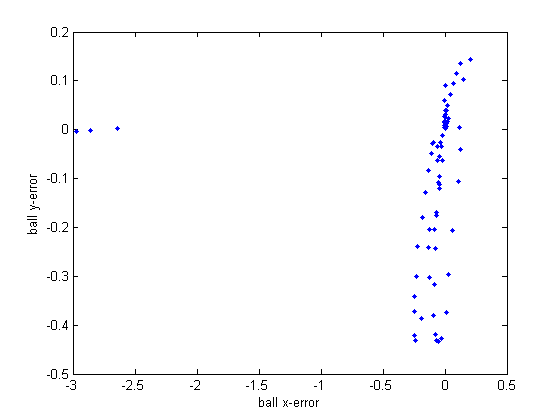
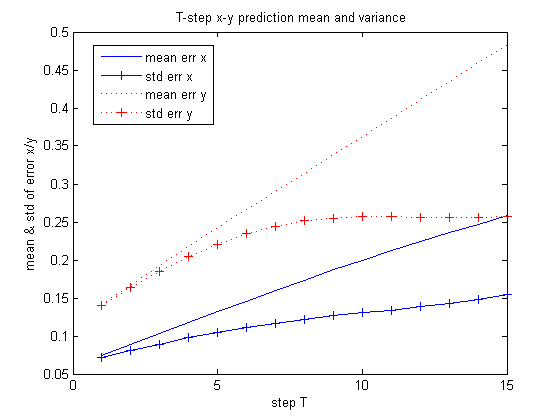
I collected the result of kalman filter and particle filter when the ball is at (.9, 0) and (2.7, 0) respectively. From the result, it seems KF is better in terms of standard error when the ball is closer. When the ball is far away, PF is better. But we may need more tests to conclude.

	# data	KF mean	KF std	PF mean	PF std
(0.9, 0)	2243	(0.7488, 0.3392)	(0.0005, 0.0009)	(0.7489, 0.3393)	(0.0018,0.0018)
(2.7,0)	7210	(3.9065,0.3168)	(0.4610,0.2817)	(3.9722,0.2829)	(0.0679,0.3811)

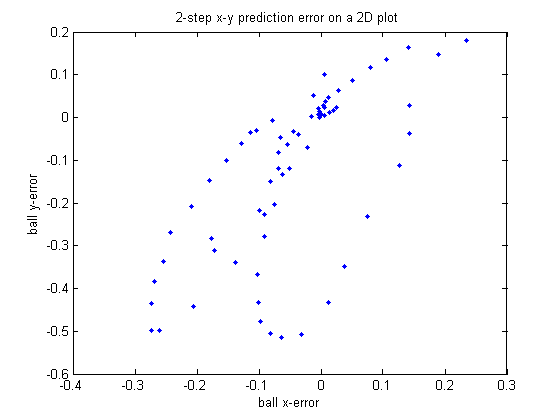
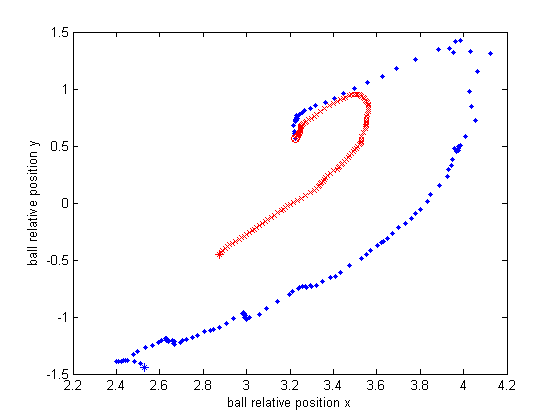
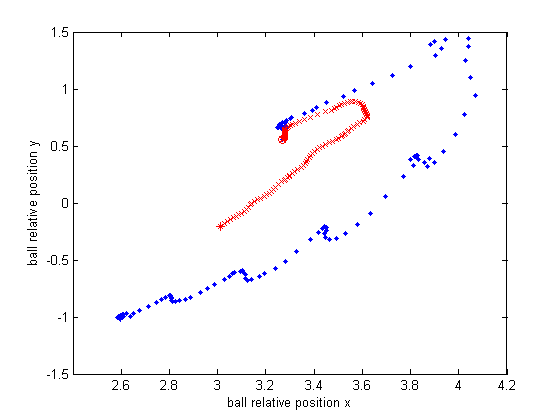
Moving-ball test setup. I kick the ball back and forth between (3.6, 0) and (3.6, -2.7). Note these two points are observed by the segway as (4.20, 0.15) and (3,45, -0.94) in the current setup. I run the test for about 3 minutes (4212 cycles) and record the tracking result of KF and PF.

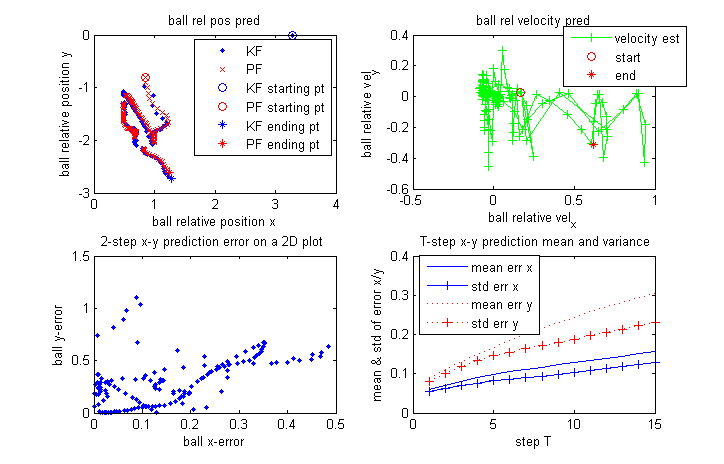
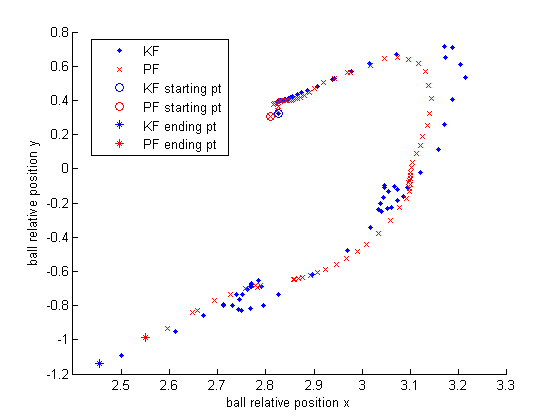
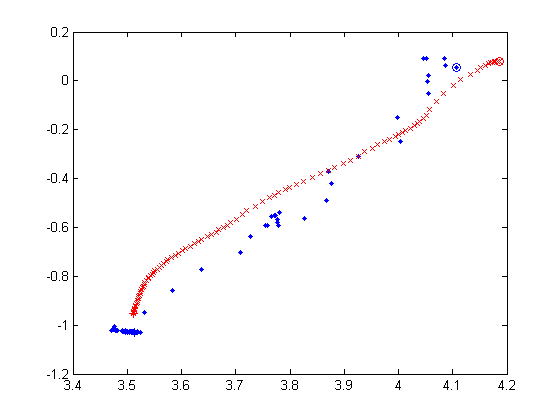
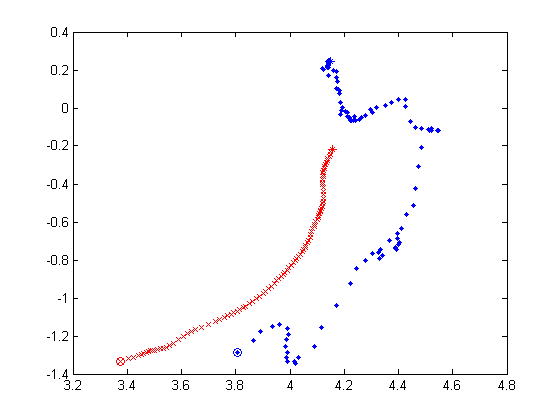
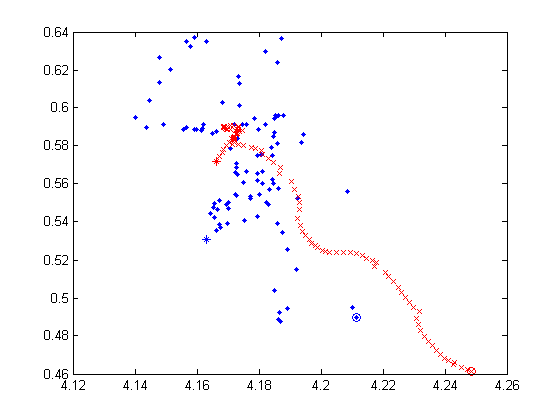
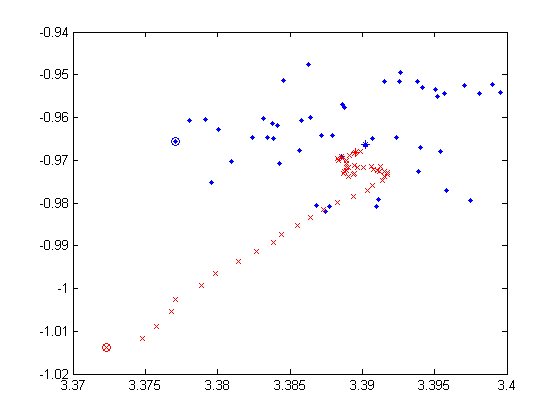
Below are 4 selected predicted trajectory of KF and PF during 100 cycles. In each plot, x/y axis is the predicted x/y relative position of the ball, the blue dot denotes the KF prediction and the red cross represents the PF prediction. And the circle is the starting point, while the star is the ending point. Though we do not know exactly the true value of each intermediate position of the ball, I kick the ball straightly and try to keep it rolling in a straight line (directly from (3.6, 0) to (3.6, -2.7). In each plot, it is obvious that PF prediction is much smoother than that of KF.






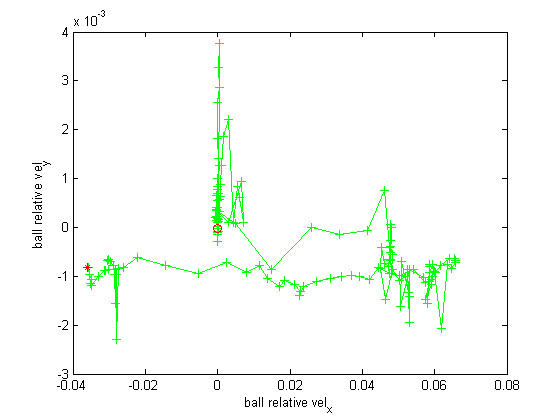
The other new feature of this PF implementation is the velocity estimation. Here are two sets of plot.
The below one is similar to the above 4 but it is during 50 cycles.

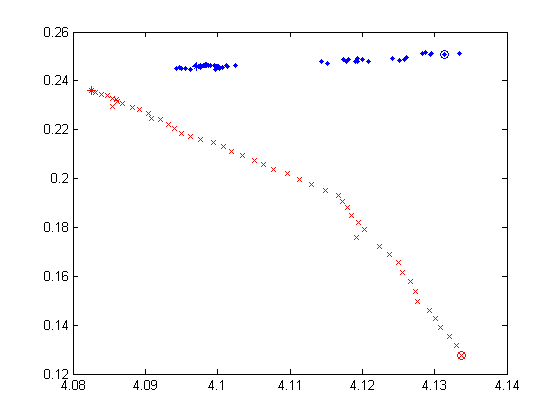
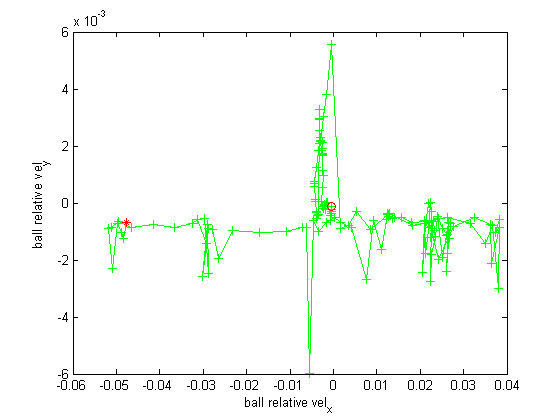
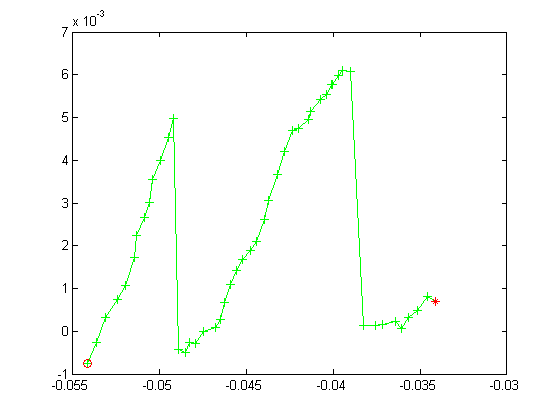
This is the corresponding velocity estimation from PF. x and y axis are predicted v_x, v_y of the ball.

Here is another set.


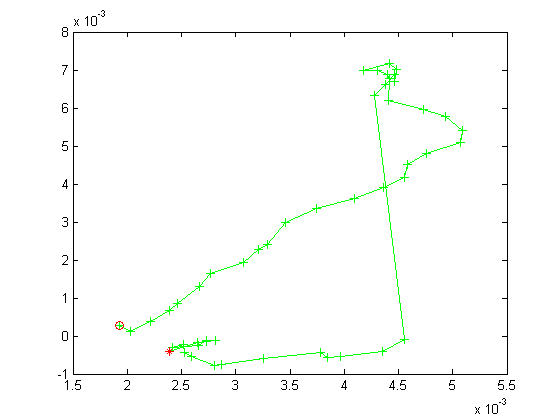
It can be seen that the predicted velocity is quite usable in these two cases.

TODO:
- test: moving robot observes static ball
- test: moving robot observes moving ball
- handle with false positive
- better movement model
- Next: tracking markers and self-localization by PF

[segway] pf draft

• world::world() ball pf tracker init
• world::updateVision(...) ball pf tracker update
• world::getBallPosition() ball pf tracker estimate
• world::getBallVelocity() ball pf tracker estimate

[debian] recursively grep

search directories recursively and print line number

# grep -rn 'IEEE1394' ./

[segway] forward declaration

from http://www-subatech.in2p3.fr/~photons/
subatech/soft/carnac/CPP-INC-1.shtml
1. B only uses references or pointers to A. Use forward declaration then : you don't need to include . This will in turn speed a little bit the compilation.

  class A ;
  
  class B {
    private:
      A* fPtrA ;
    public:
      void mymethod(const& A) const ;
  } ;

2. B derives from A or B explicitely (or implicitely) uses objects of class A. You then need to include

  #include 
  
  class B : public A {
  
  } ;
  
  class C {
    private:
      A fA ;
    public:
      void mymethod(A par) ;   
  }

[debian] purge remove

# apt-get remove libfltk1.1

Running apt-get as above will cause the packages to be removed but their configuration files, if any, will remain intact on the system. For a complete removal of the package, run:

# apt-get --purge remove libfltk1.1

[debian] change default shell

as root:

# vipw

(this will open up the password file where shells are defined per user) or

# chsh -s /usr/local/bin/bash' 

(this will change the shell for the current user to bash.)

[debian] apt-get install error

After unpacking 197kB of additional disk space will be used.
(Reading database ... 173333 files and directories currently installed.)
Unpacking sysv-rc (from .../sysv-rc_2.86.ds1-1_all.deb) ...
dpkg: error processing /var/cache/apt/archives/sysv-rc_2.86.ds1-1_all.deb (--unpack):
trying to overwrite `/etc/init.d/rc', which is also in package sysvinit
dpkg-deb: subprocess paste killed by signal (Broken pipe)

solution:

# dpkg -i --force-overwrite  
/var/cache/apt/archives/sysv-rc_2.86.ds1-1_all.deb

[debian] couldn't connect to display

happens after su

solution:

test@localhost:~$ su
root@localhost:~# xauth merge ~test/.Xauthority
root@localhost:~# export DISPLAY=:0.0
root@localhost:~# xterm # it should be fine now

reference

[segway] parameter collection for segway sim

// Camera field of view in horizontal and vertical
// in degrees

CAMERA_FOV = 94.8 70.6 // degrees

//
// This is the position of the camera with respect to the robot's
// coordinate frame (on the ground, not between the wheels)
// This is a translation of that point...

CAMERA_TRANSLATION = 0.235, 0, 1.405 // m [x, y, z] measured

//------- pan tilt settings -------------
SWAY_PAN_MIN_ANGLE = -90.0 // degrees
SWAY_PAN_MAX_ANGLE = 90.0 // degrees

SWAY_TILT_MIN_ANGLE = -88.0 // # degrees
SWAY_TILT_MAX_ANGLE = 90.0 // # degrees

[segway] noise config

BALL_Q_NOISE_OBS = [0.05 0
0 0.05];

BALL_Q_NOISE_unOBS = [10.0 6.5
6.5 10.0];

BALL_R_NOISE = [1.0 0.25
0.25 1.0];



MARKER_Q_NOISE_OBS = [1E-2 5E-4
5E-4 1E-2];

MARKER_Q_NOISE_UNOBS = [1E-2 5E-3
5E-3 1E-2];


MARKER_Q_NOISE_UNOBSABLE = [1E-3 1E-4
1E-4 1E-3];

MARKER_R_NOISE = [10.0 0.5
0.5 10.0];

WHEEL_ERROR = 0.1 m/s

SENSOR_NOISE = 1.5 m

[segway] random

there is a wrapped random generator in segway/shared/random.{cc,h}

to use it, see detail in random.h

some examples:

#include "random.h"
class random my_random;

my_random.randomize();

// gaussian distribution
my_x = my_random.gaussian32();

// uniform random number(unsigned integer) in [0, MAX)
my_y = my_random.uint32(MAX);

// uniform random number (real) in [0,1)
my_y = my_random.real32(MAX);

// uniform random number (real) in [-1,1)
my_y = my_random.sreal32(MAX);

[segway] useful previous notes

cmu smtp: smtp.andrew.cmu.edu
pop3: cyrus.andrew.cmu.edu

***linux

PCMCIA RESET
cardctl eject
cardctl insert
cardctl scheme ***

activate/deactive ethernet
ifup eth0
ifdown eth0

procedure
1. cardctl eject
2. pullout card
3. cardctl scheme
4. put card in
5. cardctl insert


/var/log : system log
/var/log/messages
/etc/pcmcia/wireless.opts
# /etc/init.d/network stop
# /etc/init.d/pcmcia restart
/etc/apt/sources.list
/etc/network/interfaces


APT: advanced package tool

choose best mirror site
netselect -vv <...>

dpkg -l pattern
dpkg --status
dpkg --listfiles
dpkg --print-avail

apt-get update
apt-get install
apt-get upgrade
apt-cache search kde


Fedora Core:
/etc/sysconfig/network-scripts/ifcfg-eth0
/etc/X11/xorg.conf (/etc/X11/XF86Config -- debian)
/etc/grub.conf


install gsl:
#./configure --prefix=/usr


***coding

uint16_t: unsigned long int

common operations of deque
.push_front()
.push_back()
.pop_front()
.pop_back()
.size()
.front()


bk citool
bk revtool
bk pull
bk abort
bk resolve -----"f" "c"

reference point: (rpos, rang)
Global -> relative: (global - rpos).rotate(-rang)
relative -> global: rel.rotate(rang) + rpos

[debian] ctags

#apt-get install ctags
to support ctags lookup in Kdevelop

[debian] knoppix again!!!

try knoppix HD-install on my laptop. Installation is easy:

get Knoppix version 3.4 or later and type

sudo knoppix-installer

in the shell !

I am downloading knoppix V3.7 2004-12-08 now via bttorrent...

Burn thd dowloaded iso onto a disc and then reboot into knoppix, open a shell and do sudo ....
Then everything is all right!
- ethernet
- wireless card
- audio
- video
- usb

Cool!

[debian] patches the new debian

- copy /etc/hosts
- apt-get install wireless-tools
- apt-get install pcmcia-cs
- shift to English shell in crxvt
export LANG=C

[segway] recompile on debian

- apt-upgrade using selection file
- install fltk
- install kernel-source-2.6.9
- #ln -s /usr/src/kernel-source-2.6.9/ linux
- change vision/V4L.h
#include "/usr/src/linux/drivers/usb/media/pwc-ioctl.h"

[debian] dpkg --get/set-selections

Record/copy system configuration

To make a local copy of the package selection states:

$ dpkg --get-selections "*" > myselections 

"*" makes myselections include package entries for "purge" too.

You transfer this file to another computer, and install it there with:

# apt-get update
# dpkg --set-selections < myselections
# apt-get -u dselect-upgrade

[segway] tracker summary

* moving objects
- 1 ball tracker
- 1 teammate tracker
- 1 opponent tracker

* non-moving objects
- 1 marker tracker
- 2 goal trackers (our side and their side)

Each tracker maintains a queue of static kalman filter.