Intro
- object的定义式是编译器为它配置内存的起点。
- 如果你想要产生一个对象数组,但该对象型别没有提供default constructor, 通常的做法是定义一个指针数组取而代之,然后利用new一一将每个指针初始化。
//class Automobile
class Autos {
public:
int cost;
int features;
int fixTimes;
Autos(int c, int f, int fix): cost(c), features(f), fixTimes(fix){}
// ...
};
Autos *ptrArray[10];
ptrArray[0] = new Autos(10000,3,2);
ptrArray[1] = new Autos(50000,2,10);
//...
copy constructor: 以某对象作为另一个同型对象的初值
string s1; // default constructor
string s2(s1); // copy constructor
string s2 = s1; // copy constructor
- pass-by-value 是calling copy constructor的同义词
- 纯粹从操作的观点来看,initialization & assignment之间的差异在于前者由constructor执行,后者由operator=执行。两个动作对应不同的函数动作。C++严格区分两者,是因为上述两个函数考虑的事情不同。constructor通常必须检验其引数的validity, 大部分assignment运算符不必如此。assignment运算符认定其参数是合法的,它会检测诸如“自己赋值给自己”这样的病态情况,以及配置新内存之前先释放旧有内存。
Item 1: Prefer const and inline to #define.
Item 2: Prefer <iostream> to <stdio.h>
Item 3: Prefer new and delete to malloc and free.
Item 4: Prefer C++-style comments.
Item 5: Use the same form in corresponding uses of new and delete.
Item 6: Use delete on pointer members in destructors.
adding a pointer member almost always requires each of the following:
- Initialization of the pointer in each of the constructors. If no memory is to be allocated to the pointer in a particular constructor, the pointer should be initialized to 0 (i.e., the null pointer).
- Deletion of the existing memory and assignment of new memory in the assignment operator. (See also Item 17.)
- Deletion of the pointer in the destructor.
Item 7: Be prepared for out-of-memory conditions.
The base class part of the design lets derived classes inherit the set_new_handler
and operator new functions they all need, while the template part of the design ensures that each inheriting class gets a different currentHandler data member.
template<class T>// "mixin-style" base class
class NewHandlerSupport {// for class-specific
public:// set_new_handler support
static new_handler set_new_handler(new_handler p);
static void * operator new(size_t size);
private:
static new_handler currentHandler;};
template<class T>
new_handler NewHandlerSupport<T>::set_new_handler(new_handler p)
{
new_handler oldHandler = currentHandler; currentHandler = p;
return oldHandler;
}
template<class T>
void * NewHandlerSupport<T>::operator new(size_t size)
{
new_handler globalHandler =
std::set_new_handler(currentHandler);
void *memory;
try {
memory = ::operator new(size);
}
catch (std::bad_alloc&) {
std::set_new_handler(globalHandler);
throw;
}
std::set_new_handler(globalHandler);
return memory;
}
}
// this sets each currentHandler to 0template<class T>
new_handler NewHandlerSupport<T>::currentHandler;
Item 8: Adhere to convention when writing operator new and operator delete.
pseudocode for a non-member operator new looks like this:
void * operator new(size_t size) // your operator new might
{ // take additional params
if (size == 0) { // handle 0-byte requests
size = 1; // by treating them as
} // 1-byte requests
while (1) {
attempt to allocate size bytes;
if (the allocation was successful)
return (a pointer to the memory);
// allocation was unsuccessful; find out what the
// current error-handling function is (see Item 7)
new_handler globalHandler = set_new_handler(0);
set_new_handler(globalHandler);
if (globalHandler) (*globalHandler)();
else throw std::bad_alloc();
}
}
Item 7 remarks that operator new contains an infinite loop, and the code above shows that loop explicitly. while (1) is about as infinite as it gets. The only way out of the loop is for memory to be successfully allocated or for the new-handling function to do one of the things described in Item 7:
- make more memory available,
- install a different new-handler,
- deinstall the new-handler,
- throw an exception of or derived from std::bad_alloc,
- or fail to return.
It should now be clear why the new-handler must do one of those things. If it doesn't, the loop inside operator new will never terminate.
pseudocode for a non-member operator delete:
void operator delete(void *rawMemory)
{
if (rawMemory == 0) return; // do nothing if the null
// pointer is being deleted
deallocate the memory pointed to by rawMemory;
return;
}
Item 9: Avoid hiding the "normal" form of new.
Item 10: Write operator delete if you write operator new.
Item 11: Declare a copy constructor and an assignment operator for classes with dynamically allocated memory.
if a class has dynamically allocated memory, but it has no copy consturctor and no assignment operator.
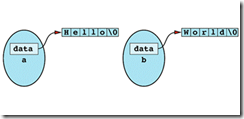
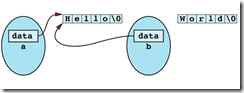
b = a;
after the assignment operation, the memory that contains "World\0" is lost!
the internal pointers in a and b both point to "Hello\0". If a's destructor is called, memory "Hello" is deleted, while b's pointer is still pointing to that memory!
Write your own versions of the copy constructor and the assignment operator if you have any pointers in your class. Inside those functions, you can either copy the
pointed-to data structures so that every object has its own copy, or you can implement some kind of reference-counting scheme (see Item M29) to keep track of how many objects are currently pointing to a particular data structure.
Item 12: Prefer initialization to assignment in constructors.
There are times when the initialization list must be used. In particular, const and reference members may only be initialized, never assigned.
template<class T>
class NamedPtr {
public:
NamedPtr(const string& initName, T *initPtr);
//...
private:
const string name;
T * const ptr;
};
This class definition requires that you use a member initialization list, because const members may only be initialized, never assigned. So,
template<class T>
NamedPtr<T>::NamedPtr(const string& initName, T *initPtr )
: name(initName), ptr(initPtr)
{}
instead of
template<class T>
NamedPtr<T>::NamedPtr(const string& initName, T *initPtr)
{
name = initName;
ptr = initPtr;
}
Note that static class members should never be initialized in a class's constructor. Static members are initialized
only once per program run, so it makes no sense to try to "initialize" them each time an object of the class's type
is created.
Item 13: List members in an initialization list in the order in which they are declared.
Item 14: Make sure base classes have virtual destructors.
When you try to delete a derived class object through a base class pointer and the base class has a nonvirtual destructor, the results are
undefined.
Item 15: Have operator= return a reference to *this.
Item 16: Assign to all data members in operator=.
Item 17: Check for assignment to self in operator=.
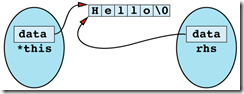
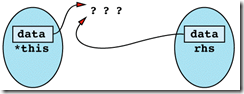
A more important reason for checking for assignment to self is to ensure correctness. Remember that an
assignment operator must typically free the resources allocated to an object (i.e., get rid of its old value) before it can allocate the new resources corresponding to its new value. When assigning to self, this freeing of resources can be disastrous, because the old resources might be needed during the process of allocating the new ones.
Item 18: Strive for class interfaces that are complete and minimal.
// return element for read/write
T& operator[](int index);
// return element for read-only
const T& operator[](int index) const;
By declaring the same function twice, once const and once non-const, you provide support for both const and non-const Array objects.
Item 19: Differentiate among member functions, non-member functions, and friend functions.
class Rational {
public:
Rational(int numerator = 0, int denominator = 1);
int numerator() const;
int denominator() const;
const Rational operator*(const Rational& rhs) const;
private:
//...
};
Rational oneEighth(1, 8);
Rational oneHalf(1, 2);
Rational result = oneHalf * oneEighth; // fine
result = result * oneEighth; // fine
result = oneHalf * 2; // fine
result = 2 * oneHalf; // error!
隐式转换可以在 non-explicite constructor 的 parameter listed in the function declaration
// declare this globally or within a namespace; see
// Item M20 for why it's written as it is
const Rational operator*(const Rational& lhs,
const Rational& rhs)
{
return Rational(lhs.numerator() * rhs.numerator(),
lhs.denominator() * rhs.denominator());
}
Rational oneFourth(1, 4);
Rational result;
result = oneFourth * 2; // fine
result = 2 * oneFourth; // hooray, it works!
Lessons: (assume f is the function you're trying to declare properly and C is the class to which it is conceptually related )
- Virtual functions must be members. If f needs to be virtual, make it a member function of C.
- operator>> and operator<< are never members. If f is operator>> or operator<<, make f a non-member function. If, in addition, f needs access to non-public members of C, make f a friend of C.
- Only non-member functions get type conversions on their left-most argument. If f needs type
conversions on its left-most argument, make f a non-member function. If, in addition, f needs access to
non-public members of C, make f a friend of C.
- Everything else should be a member function. If none of the other cases apply, make f a member
function of C.
Item 20: Avoid data members in the public interface.
Item 21: Use const whenever possible.
char *p = "Hello"; // non-const pointer, non-const data
const char *p = "Hello"; // non-const pointer, const data
char * const p = "Hello"; // const pointer, non-const data
const char * const p = "Hello"; // const pointer, const data
Basically, you mentally draw a vertical line through the asterisk of a pointer declaration, and if the word const appears to the left of the line, what's pointed to is constant; if the word const appears to the right of the line, the pointer itself is constant; if const appears on both sides of the line, both are constant.
Some of the most powerful uses of const stem from its application to function declarations. Within a function declaration, const can refer to the function's return value, to individual parameters, and, for member functions, to the function as a whole.
Item 22: Prefer pass-by-reference to pass-by-value.
Item 23: Don't try to return a reference when you must return an object.
when deciding between returning a reference and returning an object, your job is to make the choice that does the right thing. Let your compiler vendors wrestle with figuring out how to make that
choice as inexpensive as possible.
Item 24: Choose carefully between function overloading and parameter defaulting.
The confusion over function overloading and parameter defaulting stems from the fact that they both allow a single function name to be called in more than one way.
void f(); // f is overloaded
void f(int x);
f(); // calls f()
f(10); // calls f(int)
void g(int x = 0); // g has a default parameter value
g(); // calls g(0)
g(10); // calls g(10)
The answer depends on two other questions. First, is there a value you can use for a default? Second, how many algorithms do you want to use? In general, if you can choose a reasonable default value and you want to employ only a single algorithm, you'll use default parameters (see also Item 38). Otherwise you'll use function overloading.
// A class for representing natural numbers
class Natural {
public:
Natural(int initValue);
Natural(const Natural& rhs);
private:
unsigned int value;
void init(int initValue);
void error(const string& msg);
};
inline
void Natural::init(int initValue) {
value = initValue;
}
Natural::Natural(int initValue) {
if (initValue > 0) init(initValue);
else error("Illegal initial value");
}
inline Natural::Natural(const Natural& x) {
init(x.value);
}
The constructor taking an int has to perform error checking, but the copy constructor doesn't, so two different functions are needed. That means overloading. However, note that both functions must assign an initial value for the new object. This could lead to code duplication in the two constructors, so you maneuver around that problem by writing a private member function init that contains the code common to the two constructors. This tactic using overloaded functions that call a common underlying function for some of their work is worth remembering, because it's frequently useful (see e.g., Item 12).
Item 25: Avoid overloading on a pointer and a numerical type.
Item 26: Guard against potential ambiguity.
Item 27: Explicitly disallow use of implicitly generated member functions you don't want.
Item 28: Partition the global namespace.
Item 29: Avoid returning "handles" to internal data.
class String {
public:
String(const char *value); // see Item 11 for pos-
~String(); // sible implementations;
// see Item M5 for comments on the first constructor
operator char *() const; // convert String -> char*;
// see also Item M5
//...
private:
char *data;
};
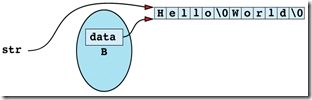
const String B("Hello World"); // B is a const object
char * str = B;
strcpy(str, "Hi Mom");
The flaw in this function is that it's returning a "handle" ? in this case, a pointer ? to information that should be hidden inside the String object on which the function is invoked. That handle gives callers unrestricted access to what the private field data points to.
Item 30: Avoid member functions that return non-const pointers or references to members less accessible than themselves.
Item 31: Never return a reference to a local object or to a dereferenced pointer initialized by new within the function.
In spite of the foregoing discussion, you may someday be faced with a situation in which, pressed to achieve performance constraints, you honestly need to write a member function that returns a reference or a pointer to a less-accessible member. At the same time, however, you won't want to sacrifice the access restrictions that private and protected afford you. In those cases, you can almost always achieve both goals by returning a pointer or a reference to a const object.
Item 32: Postpone variable definitions as long as possible.
Not only should you postpone a variable's definition until right before you have to use the variable, you should try to postpone the definition until you have initialization arguments for it. By doing so, you avoid not only constructing and destructing unneeded objects, you also avoid pointless default constructions. Further, you help document the purpose of variables by initializing them in contexts in which their meaning is clear.
Item 33: Use inlining judiciously.
Item 34: Minimize compilation dependencies between files.
Item 35: Make sure public inheritance models "isa."
Item 36: Differentiate between inheritance of interface and inheritance of implementation.
Item 37: Never redefine an inherited nonvirtual function.
Item 38: Never redefine an inherited default parameter value.
Item 39: Avoid casts down the inheritance hierarchy.
Item 40: Model "has-a" or "is-implemented-in-terms-of" through layering.
Item 41: Differentiate between inheritance and templates.
Item 42: Use private inheritance judiciously.
Item 43: Use multiple inheritance judiciously.
Item 44: Say what you mean; understand what you're saying.
Item 45: Know what functions C++ silently writes and calls.
Item 46: Prefer compile-time and link-time errors to runtime errors.
Item 47: Ensure that non-local static objects are initialized before they're used.
Item 48: Pay attention to compiler warnings.
Item 49: Familiarize yourself with the standard library.
Item 50: Improve your understanding of C++.