Trie

topCoder article: Using Tries

This data structure is used to index and search strings inside a text. Trie allows us to find words that have a single character different, a prefix in common, a character missing, etc. Running time: O(L), where L is the length of a single word.

 

 

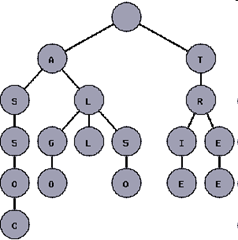
The left figure is an example from topcoder article. It shows a trie with the words "tree", "trie", "algo", "assoc", "all", and "also".

• The trie is a tree where each vertex represents a single word or a prefix.
• The root represents an empty string (""), the vertexes that are direct sons of the root represent prefixes of length 1, the vertexes that are 2 edges of distance from the root represent prefixes of length 2, the vertexes that are 3 edges of distance from the root represent prefixes of length 3 and so on. In other words, a vertex that are k edges of distance of the root have an associated prefix of length k.
• Let v and w be two vertexes of the trie, and assume that v is a direct father of w, then v must have an associated prefix of w.

 

 

My C++ Code:

#include <string>
#include <iostream>

// Interval node data structure
class Node {
    static const int m_n = 26;  // maximum number of kids
private:   
    char m_data;         // data stored at current node
    int m_prefixes;   // how many words have the prefix of the vertex
    int m_words;      // the number of words that match with a given string
    Node* m_kids[m_n];  // pointers to all its kids

public:
    // create an empty node
    Node(): m_data(' '), m_prefixes(0), m_words(0) {
        for(int i = 0; i < m_n; ++i)
            m_kids[i] = NULL;
    };

    // create a node to store data v
    Node(char v): m_data(v), m_prefixes(0), m_words(0) {
        for(int i = 0; i < m_n; ++i)
            m_kids[i] = NULL;
    };

    // copy constructor, recursively copy nodes from p
    Node(const Node& p) {
        this->m_data = p.m_data;
        this->m_prefixes = p.m_prefixes;
        this->m_words = p.m_words;
        for(int i = 0; i < m_n; ++i) {
            if(p.m_kids[i] == NULL) {
                this->m_kids[i] = NULL;
                continue;
            }
            this->m_kids[i] = new Node(*p.m_kids[i]);
        }
    };

    // print substree rooted at p
    void Print(Node* p, const std::string prefix) const {
        int nkids = 0;
        for(int i = 0; i < m_n; ++i) {
            if(p->m_kids[i] == NULL) continue;
            Print(p->m_kids[i], prefix + p->m_data);
            nkids++;
        }
        if(nkids == 0) {
            std::cout << prefix+p->m_data << std::endl;
        }
    };

    // add words rooted at p
    void AddWord(Node* p, const std::string word) {
        if(word.empty())
            p->m_words ++;
        else {
            p->m_prefixes ++;
            int k = word[0]-'a';
            if(p->m_kids[k] == NULL) 
                p->m_kids[k] = new Node(word[0]);
            AddWord(p->m_kids[k], word.substr(1));
        }
    };

    int CountWords(Node *p, const std::string word) const{
        int k = word[0]-'a';
        if(word.empty())
            return p->m_words;
        
        else if(p->m_kids[k] == NULL)
            return 0;
        else 
            return CountWords(p->m_kids[k], word.substr(1));
    };

    int CountPrefixes(Node *p, const std::string prefix) const{
        int k = prefix[0]-'a';
        if(prefix.empty())
            return p->m_prefixes;
        
        else if(p->m_kids[k] == NULL)
            return 0;
        else 
            return CountWords(p->m_kids[k], prefix.substr(1));
    };

    // recursively delete node tree
    ~Node() {
        for(int i = 0; i < m_n; ++i) {
            if(this->m_kids[i] == NULL) continue;
            delete this->m_kids[i];
        }
    };
};
// Trie data structure
class Trie {
public:
    Trie() {m_root = new Node(' ');};
    Trie(const Trie &t) { m_root = new Node(*t.m_root);}
    ~Trie() {delete m_root;};
    void AddWord(const std::string word) { m_root->AddWord(m_root, word); }
    int CountWords(const std::string word) { return m_root->CountWords(m_root, word);}
    int CountPrefixes(const std::string prefix) {return m_root->CountPrefixes(m_root, prefix);}
    void Print() {m_root->Print(m_root, std::string(""));}
private: 
    // root node
    Node* m_root;
};

int main() {
    Trie* t = new Trie();
    t->AddWord(std::string("tree")); 
    t->AddWord(std::string("trie")); 
    t->AddWord(std::string("trie")); 
    t->AddWord(std::string("trie")); 
    t->AddWord(std::string("trie"));
    t->AddWord(std::string("trieg"));
    t->AddWord(std::string("algo"));
    t->AddWord(std::string("algo"));
    t->AddWord(std::string("assoc"));
    t->AddWord(std::string("all"));
    t->AddWord(std::string("allall"));
    t->AddWord(std::string("allus"));
    t->AddWord(std::string("also"));

    t->Print();
    printf("%d\n", t->CountPrefixes(std::string("trie")));  
    printf("%d\n", t->CountPrefixes(std::string("trieg")));
    printf("%d\n", t->CountWords(std::string("trie")));
    
    Trie r(*t);
    delete t;
    r.Print();

    return 0;
}

output: 

algo
allall
allus
also
assoc
tree
trieg
4
1
4
algo
allall
allus
also
assoc
tree
trieg