Sweeping: http://www.cs.mcgill.ca/~cs251/ClosestPair/ClosestPair1D.html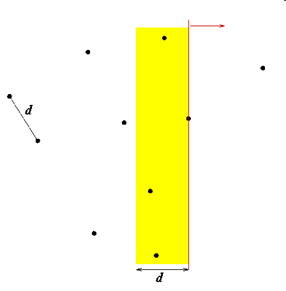
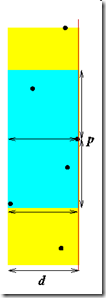
every time the sweep line encounters a point p, we will perform the following actions:
- Remove the points further than d to the left of p from the ordered set D that is storing the points in the strip.
- Determine the point on the left of p that is closest to it
- If the distance between this point and p is less than d (the current minimum distance), then update the closest current pair and d.
The summary and analysis of the plane sweep algorithm goes something like this:
- sort the set according to x-coordinates (this is necessary for a plane sweep approach to determine the coordinates of the next point), which takes O(nlogn) time
- inserting and removing each point once from the ordered set D (each insertion takes O(logn) time as shown in the section on (2,4)-trees), which takes a total of O(nlogn) time
- comparing each point to a constant number of its neighbors (which takes O(n) time in total )
K-D Tree
Animation: http://donar.umiacs.umd.edu/quadtree/points/kdtree.html
Complexity
- Building a static kd-tree from n points takes O(n log 2 n) time if an O(n log n) sort is used to compute the median at each level. The complexity is O(n log n) if a linear median-finding algorithm such as the one described in Cormen et al[3] is used.
- Inserting a new point into a balanced kd-tree takes O(log n) time.
- Removing a point from a balanced kd-tree takes O(log n) time.
- Querying an axis-parallel range in a balanced kd-tree takes O(n1-1/d +k) time, where k is the number of the reported points, and d the dimension of the kd-tree.
- Finding the nearest point is an O(log N) operation.